Chapter 9 – Mandalas of Time-Space and the Time-Space of the Transphysical Worlds
When we think about actuality, most of us usually imagine space, or space-time, as a kind of vast container populated by objects such as human beings, giraffes, galaxies, and atoms. Indeed, we tend to think of it as a kind of extended, substantial nothingness. In this chapter, I will show why this old Newtonian view of space is metaphysically unproductive and why even Einstein-inspired ideas of geometrical “space-time” are also inadequate as long as we hold on to the notion of space and time as some kind of extended emptiness. In the following pages, I will make the case that we need to radically revise our ideas of space and time (or, more accurately, unified “time-space”—as I prefer to call it, for reasons I will explain shortly) as the arena in which actual events or things take place.
· First, I will demonstrate that it is both intelligible and plausible to imagine that time-space is not neutrally “out there” (external to conscious observers), but rather that it is a relationship among actual occasions.
· Second, I will show why the particular geometrical time-space of physics, rather than being the environment shared by all actuality, is only a relationship among low-grade actualities. In fact, I will argue that all existence (including human life and death) is played out in the context of a much more complex and interesting time-space structure. And, further, once we expand our metaphysics to include this more elaborate understanding of different kinds of time-space, the task of explaining survival of personality after death and reincarnation becomes much easier.
This chapter will probably be the most challenging of this book, and arguably the most important. I intend to spell out my arguments clearly and as simply as I can. Nevertheless, because many of the core ideas proposed here will be unfamiliar to most readers, I encourage you to take sufficient time to grasp and digest them. It may well serve you to read this chapter a second time. The ideas presented here amount to a radical reorientation of our fundamental way of understanding the world. I expect that many readers will—at least initially—find themselves caught in a recurring tension between habitual ways of thinking about space and time and the novel insights developed in this chapter. But getting out of the old mindset is crucial for understanding the metaphysical model developed in the rest of this book.
If we are going to expand science so that it can account for phenomena such as survival and reincarnation, I believe we have no option but to revise our fundamental cosmology to include what I have been calling the “transphysical worlds.” And this will require a radical revision of our understanding of time-space—beyond what we have inherited from physics and from scientifically informed common sense. Making this difficult paradigm leap, I believe, is the most important obstacle we have to overcome.
Space, Time, and Time-Space
I will begin this examination of time and space by dealing with a common misconception. Our scientific education, which is still deeply influenced by the ideas of classical physics, leads us think of space and time as if they are somehow separate from each other. Scientifically, we have the idea that reality exists at any single instant as a spatial configuration of matter. In other words, take away or freeze time, and space with its distribution of objects would still persist. Underlying and related to this assumption, we have the idea, philosophically, that space is “objective” while time is “subjective.”
In the twentieth century, Einstein’s special theory of relativity gave us a new understanding of space and time based on the realization that, in actuality, there is no movement in space that is not also a movement in time.
Einstein came to this conclusion through a long chain of reasoning when he attempted to explain the movements of light in a vacuum. This idea revealed the perplexing relations between time and space that famously emerge in relativity theory. Notwithstanding the profound advances in physics that resulted from Einstein’s insights and equations, the mind-boggling conundrums of relativity obscured a simple fact: The interconnectedness of space and time is also deducible from commonsense understanding.
Imagine two large rocks spaced well apart on a field. I am standing at one rock, and I ask “how far away is that other rock?” The distance between this rock and the other one determines how long it will take me to walk there. The greater the distance, the longer the walk. So there is some important relationship between movement, time, and distance. Now, suppose I could walk infinitely fast. Then it would not take any time for me to get from here to there. But if it doesn’t take any time for me to get from here to there, then here and there are essentially the same place, and so distance between them would be meaningless. An entity that could travel infinitely fast would have no experience of distance, and, thus, no notion of extended space.
Influenced by classical physics, we tend to think of space as more fundamental than time, and, following Einstein, physicists now often reduce time to a dimension of space. But when we think more deeply about this, it becomes clear that time is actually more fundamental than space. We can imagine time without movement, or we could imagine time with infinitely fast movements, but we can imagine space only where velocity of movement has a finite limit (whether we imagine this as a movement of bodies or a movement of causal influences). Only in the context of finite velocities does space exist at all. Time, therefore, is more fundamental than space, and because of this I choose to refer to the complex of time and space as “time-space.”
Time-Space: Scientific and Experiential
As we begin our investigation of time-space, the first thing I’d like you to notice is a bifurcation in our ordinary, scientifically informed, commonsense notions. On one hand, we have the mathematically defined space-time of physics. We imagine this to be self-subsistent and objective—in the sense that it would still be there even in the absence of any entities occupying it, and in the absence of any consciousness whatsoever. And, even in a relativistic framework—where time-space is said to be conditioned in important ways by moving masses within it, and where, therefore, time-space, matter, and energy are shown to be intrinsically interrelated—there is no mention of consciousness.[1]
On the other hand, we are all familiar with the very different “inner time-space” of our actual experience. Let us examine , for example, time-space as it presents itself to our visual sense, and contrast the physicsts understanding of time and space:
• Visually, time-space is bounded by an outer edge of what we can directly see. By contrast, the space of physics has no outer boundaries, and is either infinite or closed (which, in this context, means that if you go far enough in any one direction you will end up coming bak to where you started).
• In the time-space of perception (in all senses, including the visual), we are always dead center, always at the origin of our own set of coordinates. By contrast, in the time-space of physics there is no privileged point in this same sense. The time-space of physics is isomorphic. Every point in time-space is exactly like every other point. But the time-space of experience is an-isomorphic. In the time-space of experience, the center is a privileged point, and there are qualitative differences between what is “in front,” what is “behind,” what is “above,” what is “below” and what is “to the side.”
• The time-space of experience is fragmented, or discontinuous, in the sense that the contents of our experience are not necessarily mutually interrelated in terms of a single time-space relationship. For example, a given moment of experience may include memories from various time-space regions of waking reality, only loosely interconnected by a common feeling tone, memories of experiences that took place in dreams, and purely imaginal experiences. The relations among these different perceptual entities cannot be expressed in geometrical terms. How many miles would I have to cover to visit the magnificent castle I saw in last night’s dream? By contrast, entities in a mathematical time-space are all interrelated by the simple geometrical relation of distance.
The Relationship Between Scientific and Experiential Time-Space
What, then, is the relationship between these two time-spaces—the smooth, geometrical, infinitely extended, isomorphic time-space of physics, and the rough, bordered, anisomorphic, conceptually elusive, time-space of perception?
It is usually assumed that the time-space of perception is, through some mysterious process, generated by causal processes in the outer time-space of physics. In other words, the time and space that I subjectively perceive is assumed to result from various complex interactions between my nervous system, my sense organs, and the rest of the objective external world. The major efforts of cognitive neuroscience are directed at producing some plausible way in which energy and matter operating in mathematical time-space can generate not only representations of themselves in perception, but also generate consciousness itself. The idea is that the “real thing,” the ontologically privileged domain, is “outside” in mathematical time-space, whereas perception (all that exists subjectively “in here”) is either epiphenomenal or derivative.
I want to suggest that this approach is decisively backwards. That is, if our explanations are to be empirical, we have to ground those explanations in what we actually experience. And what we actually experience is the “inner” world of perception.
Current scientific explanation leads us into a curious impasse. It tells us that the real world exists outside experience, and that it consists of atoms, energies, or collapsing waves of probability all operating in a smooth, continuous, geometrical time-space. This is all very interesting, and it allows us to predict and control many features of the physical world. But there’s a problem—indeed the now infamous “hard problem”—namely that if the real world actually is what science describes, then there is no coherent way of accounting for the emergence of consciousness, and, thus, no way of accounting for our experience of the world at all. Thus the scientific story seems to undercut the very existence of conscious experience while, simultaneously, claiming that science is empirical, and so rooted in the actual, conscious experience of scientists.
There is, however, a way out of this impasse, and it has been articulated in the works of Ernst Cassirer[2] and Alfred North Whitehead.[3] They both set out to show the precise way in which fundamental scientific ideas are, in fact, developed by a process of abstraction that brings to our conscious attention certain invariant features of our direct experience. Thus both the everyday objects that populate our lives, and the scientific objects (such as electrons and quarks) that populate our scientific explanations can be understood as ways of recognizing and naming permanences within experience, rather than hypothetical realities outside experience.
Let’s return to our examination of the perceptual world. I suggest that we can understand experiential space by describing it as a mandala. (Mandalas are complexly structured, more or less symmetrical, images, and are a central motif in Eastern religious art. They also play a large part in Jungian psychological symbolism, where they are interpreted as representations of psychic wholeness. As I noted above, our actual experience of time-space is always centered on a privileged point—the point defining the here and now. (Technically, because we’re dealing with time-space, it’s really a “point-instant,” or, more accurately, a “moment-point.”) The rest of the world is structured for us as a display around this point. In other words, the world shows up for us as a mandala, always intrinsically coherent, with each of us at the center point of conscious perception.
We are each at the center of our own experienced world, from which we apprehend a variety of entities arrayed around us in a mandala-like configuration—the time-space of our experience.
I am proposing that this mandala-like structure of experience is the actual time-space in which the world unfolds its creative advance. In other words, perceptual space is not derived from events in outer, geometrical space. Rather, perceptual time-space is time-space itself, and geometrical space is just an abstraction that allows us to describe certain invariant relations that we can recognize and name in the perceptual time-space from which it is abstracted.
Having explored this issue in a phenomenological way, let us now look at it in terms of the ontology of actual occasions being developed in this book.
The key to this exploration is the notion that each actual occasion contains, or “houses,” the entirety of its past. This is a difficult notion to grasp because we are accustomed to thinking of things, or substances, or events as being contained, or “housed” in time-space, and I am suggesting that we reverse the figure/ground relationship.
We know that we each have our own experience of the world.
· From the purely subjective point of view, I can say that my world exists in my experience. The world that I see, for example, disappears when I close my eyes.
· Most of us, at some time, have played with the idea of solipsism, the idea that the entire world is just a figment of one’s imagination.
Without absolutizing either of these ideas, I want to suggest that they both point to an important aspect of truth. The world as I know it is contained in my experience. Even the objective world can be understood to consist of experiences that I have, and ideas that I entertain about those experiences, and is, in this sense, contained in my experience. In the modern world, and in the context of a substance ontology, the fact that the world is, contained in my experience is easily dismissed. My experience, after all, is either epiphenomenal, or it consists of qualities characterizing the mental substance that is my mind. Remember, that in a substance ontology, a substance is something that needs nothing other than itself to exist. The qualities of a substance belong to it alone. So if my varying experiences are just qualities inhering in the substance of my mind, then there is no intrinsic connection between my experiences and the qualities of other substances outside me.
We usually imagine that the our brains are part of the one physical world, and that the external causal processes bring about electro-chemical configurations of my brain that are somehow (quite miraculously) converted into conscious experiences. But in the ontology we are developing here, we are making the assumption that there are no substances and qualities in the old sense. Rather there are processes of relationship. Concrescences are the coming together of past experiences and timeless possibilities, and the character of an actual occasions consists of simple eternal objects brought together in a complex pattern. Causal transmission of energy is, according to process metaphysics, a transmission of experience through the creative advance.[4] That which causes me is that which I feel. We no longer have a situation in which efficient causality on one hand, and consciousness, on the other hand, inhabit different ontological domains—rather efficient causality and feeling are inseparable from one another, two sides of the same coin. In this sense, causal expressions of past occasions are felt in, and only in, the experiences of occasions that follow it in the creative advance. When we imagine our experience to be a mere representation of the outer world, then it is as if we are in a glass bubble, and some outer reality is being selectively represented on the surface of that bubble. I am saying there is no bubble. Our experience is the real thing.
Actual occasions have their moment of subjective immediacy, and then they expire into “objective immortality.” Their effects are felt by subsequent occasions. Each occasion houses, or contains, the causal expressions of its past. It actualizes, and then its causal expressions are felt by actual occasions that occur in its future. Each occasion houses its past, and is, in turn, housed by future occasions.
Outside this process, as Whitehead says, “there is nothing, nothing, nothing, bare nothingness.”[5]
Because each actual occasion houses its own causal past, and because actual occasions are contained only in other actual occasions, we can now say intelligibly that each actual occasion is a creative unit of time-space.[6]
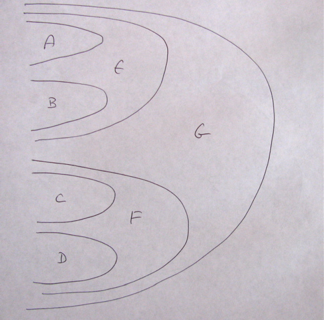
Figure 1: In this highly simplified diagram, each parabola represents an actual occasion. The past is on the left, the future is on the right.
Figure 1 (above) is a very abstract picture of the creative advance. Each parabola represents one actual occasion.
· Each actual occasion in the diagram contains, or “houses” the entirety of its causal past, and is, in its turn, housed by the occasions of its future.
· The space inside the parabola is mandala space. The center around which each actual occasion constructs its own mandala (the point of the parabola) is its mental pole, its own consciousness.
· What we have been thinking of as “external space,” or the “substantial extended nothingness” in which things take place is no longer necessary. Actual occasions are simply contained in subsequent actual occasions.[7]
· The geometrical properties of time-space are, however, still important. But rather than being properties of the “substantial extended nothingness,” they are now understood as patterns of causal relations among actual occasions. We will discuss the importance of these patterns later in this chapter.
An interesting result of this analysis is that it creates an intrinsic connection between time-space and consciousness. Scientific work in the past century has demonstrated a deep connection between time-space and energy. But if time-space consists of actual occasions, and if actual occasions are structured around a mental pole—a pole of consciousness—then time-space itself cannot be separated from consciousness.
What distinguishes “experience” from mere existence of objects is (along with aim or purpose) the factor of existence that we call “consciousness.” Whenever we prehend anything, we are aware of what we prehend. In a very important sense, consciousness, which pervades and contains all that we know, is the time-space in which experience unfolds. This brings us one step closer to a truly unified theory that shows the fundamental coherence of time-space, energy, and consciousness.
Because our experiences of the waking world are transmitted to us through our bodies, and because our bodies consist of occasions that feel, interpret, and decide, a considerable amount of interpretation intervenes between us and the waking world in itself. This leads us to posit two different modes of experience.
First, we experience the world in the “mode of causal efficacy,” which is to say that every actual occasion in our past has some, however negligible, causal effect on the structure of our experience.
Secondly, we experience the world in the “mode of presentational immediacy,” which is to say that as our experience of the actual world is interpreted in the process of concrescence, we form an interpretation, or an “appearance,” that shows us the world in a way relevant to our own history and our own purposes. This takes place for any actual occasion in any actual world. In our waking world (which we discussed in Chapter 7), we objectify the waking world through the occasions making up our bodies. Our bodies, then, are deeply involved in structuring the way in which the waking world is immediately presented to us.
This does not change the general principle: What is in our experience is the actual world out of which we grow. Even the occasions of our own bodies, the objectifications of which dominate our waking perception, are other occasions of experience in the actual world.
The Relational Theory of Time-Space
The metaphysics of Newtonian science posits the existence of absolute space and absolute time. It treats space and time as if they are actualities in their own right. Leibniz, on the other hand, developed a relational theory of space and time that reduces space and time to the status of relations among actualities. The idea of time-space I am developing here is, like that of Leibniz (and Whitehead), a relational theory of time-space.
This is an important issue, so let’s take a moment to emphasize its significance. In general, science and common sense grant time-space the status of an actuality. We tend to think of space and time as empty expanses that “contain” all other entities, and also, it is assumed, that impose certain geometrical forms on actualities (shapes) and other geometrical relations (distance) among those entities.
If, however, we try to imagine empty time-space as “extended,” we run into some interesting difficulties. For example, we find that to make the idea of extension intelligible, we must call on some notion of plurality. A single point is not extended, so extension must involve more than one point. Or, to put it another way, we cannot call space extended unless we can imagine it as a plurality of points. But can we, in fact, imagine a collection of unextended points?
Leibniz articulated a fundamental principle of logic that he called the “principle of the identity of indiscernables.” This principle states that every individual actuality, or every individual object of attention, must be different from every other entity if it is to be recognized as such. In other words, if we say that there are two entities, but that there is nothing whatsoever that distinguishes one from another, then there are not, in fact, two entities. There is only one.
If we apply this to empty time-space, which is entirely isomorphic and in which all points are identical, then there is no way to differentiate one point from another. In this case, by the principle of the identity of indiscernibles, our collection of points collapses into a single, and entirely unextended, point.
The conclusion is that time-space, to be extended at all, must be a relationship among entities that are somehow discernible one from another. Whitehead and Leibniz, each in his way, offers occasions of experience or “monads” as the entities that are needed. Time-space is, thus, a systematic pattern of relationship among actual occasions.
A relational theory of time-space is inherent in postmodern science. In the Newtonian theory of time-space, distance is a function of position only, and position is a function of placement within absolute space and absolute time. In the special theory of relativity, there is no absolute space and time, and the distances between enduring entities is a function of their positions and their velocities. Thus the configuration of time-space is a function of the dynamic relations among actualities. What is invariant in the special theory of relativity is the causal order among occasions. That is, if A caused B, then the fact that A caused B is invariant in all frames of reference.[8]
The time-space of special relativity makes distance dependent on relative velocity, and so it is relational rather than absolute. Nevertheless, it enables us to trace the causal order among occasions and so to order the past in a particular, generally unambiguous way.
The general theory of relativity is even more relational. In this theory, gravitation is imagined as a “curvature” of time-space, and that curvature is a function of the distribution of mass/energy.
Finally, in quantum mechanics, with its abrupt and statistically uncertain transitions of position, we encounter situations such as that in Figure 2, where occasions A, B, and C are contemporary, B and C (but not A) are in the immediate past of occasion D, but both A and D are in the immediate past of E. In this situation, an entity in the distant past (A) can objectify in the present (E) without having been objectified in any of the other occasions intervening between A and E. The importance of this relation will emerge when we discuss memory below.

Figure 2
In general, for purposes of science and of common sense, we can model the positions of actual entities by points, and the distances between actual entities as lines. A set of postulates specifying relations between points and lines is a geometry. Newtonian mechanics, Einsteinian physics, and quantum mechanics each posits a somewhat different geometry of time-space.
From this discussion, then, we can conclude that the structure of time-space—the geometry that defines both position and distance among points—is not absolute, but is, rather, a function of relations among occasions.
Time-Space, Causality, and Memory
We will now consider the relationship between occasions from another perspective. According to process metaphysics, to be the subject of an efficient cause is to have an experience. What I am experiencing is the objectification—or causal expression—of the prior experiences of past actual occasions. I receive those experiences into myself, I interpret them, sometimes I modify them, and then I transmit them to future occasions. Thus, the transmission of energy is always the transmission of experience. In this sense, all objective experience is the experience of past experiences. In general, that’s what memories are: experiences of past experiences.
Given the finite velocity at which efficiently causal transmissions propagate,[9] all of my experiences of other actualities are of past experiences. Some of those experiences are experiences of occasions I now identify as having been “me” in the past. We usually reserve the word “memory” for those particularly intimate experiences of our “own” past experiences. But, in principle, experiences of my own past experiences are no different from experiences of past experiences originating from a more remote source—“my” past experiences are simply more intimate. The point is that efficient causation and memory are, at this level, one and the same.
In previous chapters, I used the term “prehension” to refer to the basic connection between actual occasions. What emerges from this discussion is that prehension is a very basic notion, from which we can abstract three crucial features of actuality:
· Containment: Each occasion can be said to contain, or to extend over, all of the occasions in its past, which it prehends.
· Efficient cause: Each occasion is, in part, the outcome of the efficient causes reaching it from the past. To prehend a past occasion is to be efficiently caused by that occasions
· Memory: To be efficiently caused by a past occasion is to have an experience of the experience of that occasion. If we define memory as the experience of a past experience, then to prehend a past occasion is to remember it.
This way of regarding the primitive relationship among occasions has three significant advantages:
· First, it allows us to abandon any attempt to explain memory by a neural trace theory. There is no need for any physical record in the brain to explain memory. Memory is just the objectification of a past occasion in a present occasion. Because all of the past is causally effective in the present, there need be no special route of transmission to connect a memory to a present occasion.[10]
· Second, we don’t have to construct some elaborate theory to account for parapsychological phenomena in terms of physical causes; rather we can now construct an account of how intrinsically parapsychological relations are limited and restricted so that they function as physical causes in the inorganic world. Every efficient cause is an experience of a past experience, including all of the feelings of “emotion” and “meaning” that characterized the occasion being prehended. A mental-grade occasion will objectify in a future mental occasion in a way that is a direct transmission of meaning—a telepathic interaction. A medium-grade occasion will objectify itself in a future medium-grade occasion which is a direct sharing of emotion—an empathic interaction. Low-grade, inorganic occasions will objectify in future low-grade occasions as physical interactions, as simple forms or facts in the mode of sense certainty. This is efficient cause as understood in modern and postmodern physics. In process metaphysics, however, there is no longer any need to look for a “physical mechanism” that can account for empathy and telepathy. Rather the very mechanism of efficient cause, so important in all physical explanation, is now expanded so that, depending on the grade of the occasions involved, it can function as a simple transmission of physical fact, as an empathic interaction, or as a telepathic interaction.
· Third, memory, we have seen, is a direct sharing of experience. Empathy, telepathy and empathy can now be understood as different modes of memory.
The Ordering Function of Time-Space
Whitehead holds that each nascent occasion feels (or, in his technical language, “positively prehends”) every actual entity in its past. As this chapter develops, and we discuss what I will call “extensive networks,” we will come to see that, in fact, an occasion need not feel each and every occasion of the general past, but—assuming we allow for extremely trivial experiences—then it seems obvious that every occasion must feel the entirety of its causal past.
However, although every actuality in my casual past does have some, however minimal, effect on me, the occasions of my immediate past are still distinguishable from the occasions of their immediate past, and so on. This because the occasions of my immediate past contain experiences of events in the more distant past, but occasions of the more distant past do not contain experiences of the immediate past. In this way, we can speak of spatiotemporal distance, and we can (as we do in relativity theory) sort the past into a meaningful, causal order.
I propose to call this causal ordering of the past the “time-space relationship”—and it plays a number of important roles in the creative advance:
· Every society, or self-organizing system, of actual occasions must share a common time-space relation. Since we usually assume that all of actuality operates in terms of one, and only one, time-space relation, we usually don’t have to state this condition. But in transpersonal process metaphysics, there may be many time-space relations functioning in parallel, or overlapping in complex ways, and so it becomes necessary to point this out.
· The time-space relation characterizing the occasions in a society serves as a “system of indication.” A system of indication is a set of systematic relations among actualities that allows us to use terms such as “this one,” “that one,” “over there,” “the one I saw yesterday” and so forth. Without a scheme of indication that allows us to designate particulars for each other, we could not form propositions such as “that ball is blue.” [for Glossary] Also, in the transmission of experiences through the nervous system, it is important that successive occasions can recognize inputs from various other occasions as pertaining to the same actualities outside the body. This is an aspect of the “binding problem.” For example, I see a bell, and I hear a bell, and both the high-grade occasion that is me and the occasions that are my eye consciousness and ear consciousness must all recognize the visual and the auditory impressions as belonging together so that they can be “bound” into a single experience of the bell. They can perform this function only if they share some systematic way of designating particulars.
· The time-space relation conditions the transmission of causal efficacy. Much of our science is concerned with the idea of the attenuation of causal efficacy with increase in distance (for example, gravitational and electromagnetic influences fall off with the square of the distance), and distance is always a relation (not necessarily mathematical, as we will see) defined by the time-space relation.
In physics, the time-space relation is what I referred to in the last section as a particular geometry. Thus, we could say that classical physics, relativity physics, and quantum physics each describes actuality in terms of a different time-space relation. In the next section, I will say more about the relationship between possibility, actuality, and the time-space relationship.
Possibility, Actuality, and the Time-Space Relationship
In Chapter 4, I discussed the relationship between possibility and actuality in terms of the relationship between forms and events (which I have also been calling eternal objects and actual occasions). We saw that each occasion becomes actual by deciding, in each situation, which of the possibilities opened to it will choose. Actualization is a process of decision (or “cutting off”) that narrows the possibilities until only one is left.
Now let us focus on the structure of the field of possibility itself. But first: What is a “field of possibility”? The simplest way to understand this idea is to think in terms of what scientists call “natural law.” If we know a natural law, then, given a particular set of circumstances to which the law applies, we know the range of possibilities relevant to the immediate future of that situation. Suppose I am standing on the surface of the Earth, and I am holding a rubber ball in my outstretched arm. My knowledge of the laws of gravitation give me a very accurate idea of where the ball will go, and of how fast it will go there, after it is released. My knowledge of natural law is useful because it lets me know the field of possibilities that extends outward from the current event that is my experience in this moment.
Any actuality is, of course, much more complex than any set of mathematically expressed natural laws could ever encompass, but nonetheless it is clear that what happens in our experience is always relevant to, and conditioned by, what has already happened. There is a structure of possibility.
We also saw in chapter 4 that the eternal objects (or forms of definiteness), that we prehend in the world and in our thoughts, are possibilities. A specific eternal object is the just the possibility that some actual occasion might possess that particular character. Thinking is the process whereby we recognize the possibilities that were actualized in the past and that may be actualized in the future. Logic, as an order among abstractions, is also an order among possibilities. Thus, we can fruitfully imagine the structure of possibility as analogous to a logical system. This is important because logic also applies to actuality. The first principle of any philosophy that hopes to find rational order in the universe must be that actuality is logically consistent with itself, which is to say that what happens next must always be logically consistent with what has already happened. This does not mean that nothing new or novel never happens—it just means that whatever novelty does arise cannot contradict the actuality of the past out of which it arises.
Now let us look at the structure of possibility as analogous to the structure of a logical system. As we construct such a system, we begin just with possibility itself, a kind of blank slate on which various logical systems can be written. Then each definition and each axiom that we introduce closes down the field of possibility by limiting it to certain conditions. The more axioms and definitions we introduce, the narrower the scope of the possibilities they define. For example, we could begin our process by defining the notion of a thing, a finite natural being, or an enduring entity. This excludes all things infinite, and all mere flashes of existence. I could further narrow the field by specifying plants, as opposed to animals and minerals, and then narrow my definition still further by including only flowering plants, and so on. It would seem natural that when all of the generality has been squeezed out, and everything that needs to be determined has been determined, we ought to find a single actual event being singled out.
This is, indeed, Whitehead’s idea. A given situation presents some set of possibilities, all of which are compatible with the past, but many of which are incompatible with each other, and so incapable of joint realization. An actual occasion, in its process of coming to be (its concrescence), makes decisions eliminating more and more possibilities until it becomes perfectly definite, at which point it is actualized.
This position suggests that the process of abstraction can proceed in two very different directions.[11] If we start with a very complex actual occasion, any abstraction from that will involve a simplification and a loss of “information.”[12] For example, my knowledge of the person next to me can be very full, very rich, and relatively complete. I can feel that person, smell that person, hear that person breathe, and see every pore on his or her face. We could say that my knowledge is relatively close to the concrete actuality of that person. But, by contrast, my knowledge of a fellow spectator sitting across the field from me at the stadium is very abstract. I know him or her as “just a person.” Abstracting from actuality leads to simplification, a loss of information.
When, however, I abstract from a logical system, or a structure of possibility, what I end up with is a set of abstractions that is fuller and richer than the one I started with. For example, suppose we start with arithmetic. Arithmetic is important because all so-called higher math builds on the foundation of arithmetic. In other words, the structure of arithmetic is assumed by trigonometry, calculus, and so on. So if we abstract from all forms of “higher math” we will find ourselves left with arithmetic.
But we can also abstract from arithmetic, as Peano did in the early twentieth century. He found that he could deduce all the theorems of arithmetic from just three definitions and five axioms[13] —provided we assume the postulates of propositional logic as a background. This is certainly an economy of expression, but it is much more than that.
First of all, in this mode of abstracting there is no loss of information. All of arithmetic can be derived from Peano’s postulates and definitions. In addition, abstracting from sets of structured possibilities in this way opens us up to great ranges of alternative possibilities. For example, once we have seen that all of arithmetic can be grasped in terms of three definitions and five axioms, we have opened up a vast meta-arithmetical realm. We can now experiment with different sets of definitions and axioms, each of which opens up a new realm of order, and see whether those new forms of order might have application in actuality.
Science is the attempt to identify the particular characteristics of the actual situation in which we find ourselves. We express this character in the form of logical propositions. But sets of logical propositions can be more or less general, and, thus, they can allow the occasions they govern to be more or less free.
We have seen that each actual occasion contains the entirety of its own causal past, and prehends that past as ordered by a particular time-space relationship. We have seen, too, that in terms of a postmodern, relativistic understanding of time-space, this ordering of the past is essentially causal—i.e., an understanding of the time-space relation allows us to see which occasions have affected which other occasions in the past and, from that, to predict (probabilistically) where and when causal actions will have effects in the future.
The causal order among actual occasions can be, for many purposes, represented in terms of points and lines, and sets of propositions concerning the interactions of points and lines form various geometries. These geometries, as we will see in detail in the following section, may have greater or fewer propositions, and so may be more or less general.
Let’s pause here to review the main points covered so far in this chapter:
· We began by observing that even in terms of both relativity theory and common sense, the very notion of space is undefined except in situations where movement (or causal propagation) is restricted to some finite velocity. Also, time is more fundamental than space, so that we are calling the complex of time and space “time-space.”
· We explored the nature of experiential time-space, and saw that it can be described as a mandala—an array of meaningful events coordinated around a privileged center. Every actual occasion—every drop of experience—apprehends its world in this mandala form.
· We then considered the relationship between mandala time-space and scientific time-space, and concluded that of the two, mandala time-space is more fundamental. Each actual occasion, within its mandala of experience, “houses,” or contains the entirety of its causal past, and is, in turn, contained within the occasions that will make up its causal future. Outside this mutual containment, there is nothing whatsoever. In other words, actual occasions are not contained or housed in some neutral extended nothingness, rather they are contained or housed in each other so that each is a creative unit (or “atom,” as Whitehead would say) of time-space.
· These considerations led us to a relational theory of time-space—an idea originally suggested by Leibniz and further developed by Whitehead. We saw that we can understand points as abstract representations of actual occasions, and lines as abstract representations of relations among actual occasions (prehensions). Geometry is, at least in part, a study of relations among points and lines and, as we now know, there are many different geometries. Thus, there can be any number of different time-spaces in terms of which actuality can function.
· The primary ordering among occasions in a post-relativistic frame of reference is their causal ordering—i.e., we order our past primarily in terms of which occasion was in the causal past of each other occasion. We saw that this ordering can be understood in terms of containment, efficient cause, or memory.
· The way in which we order the past serves as a “scheme of indication,” or a way of pointing to, or designating, particular facts and also of orienting ourselves in the systematic network of causal interactions pervading the actual world.
· We saw that the geometries in terms of which we order the past (and, of course, anticipate the future) can be more or less constraining as they involve greater or fewer definitions and axioms. Thus, as we will see, there is a hierarchy of geometries, moving from the metrical geometries at one end, to “extensive networks” at the other.
Given these considerations, given the data of parapsychology and the evidence for re-incarnation and personality survival that we discussed earlier, and given the hopeless inadequacy of modern materialism to account for any of these phenomena, it now becomes plausible, as we saw in the last chapter, to hypothesize the existence of different grades of actual occasions forming different transphysical worlds. I now propose that each of these worlds is differentiated from the others because occasions of different grades interact in ways that define different geometries, or different time-spaces. In other words, it now becomes plausible to begin the process of forming a mathematical analysis of the time-space of the transphysical worlds.
The theory being advanced here is that an adequate description of reality requires us to posit both a physical (inorganic) world, and several transphysical worlds. The simplest, most abstract, of these worlds is the physical domain studied by modern physics. This world consists of a system of low-grade occasions defining, through their causal interactions, a time-space relation that can be characterized by a metrical geometry. Each transphysical world consists of a system of higher-grade occasions defining, through their causal interactions, geometries that are much more general and, thus, freer, than the geometry of the physical world.
Our next task, then, is to look at different varieties of geometry, so that we can get a better sense of how these transphysical worlds might function.
Varieties of Geometry
Geometry is the logical expression of a time-space relation. The fewer the postulates governing the time-space relation, the more general it is. The “higher,” or “more transphysical,” a world is, the higher the grade of the occasions involved, and the freer and less constrained is the time-space relation. The discipline of meta-geometry illustrates this principle.
Our modern commonsense understanding of the logical structure of time-space is still Euclidean and Cartesian. We think of the time-space relation as being expressible in terms of three spatial axes, each perpendicular to the others, and one temporal axis perpendicular to the other three.
The axioms of Euclid, the basis for Descartes’ analytic geometry, include a particular parallel postulate: Given any straight line and a point not on it, there exists one, and only one, straight line that passes through that point and never intersects the first line, no matter how far they are extended. In short, parallel lines never meet.
One of the most significant intellectual events of the past few centuries was the discovery that there are perfectly valid geometries other than the Euclidean and, therefore, perfectly valid time-space relations, in which the parallel postulate is violated. Thus:
· In Euclidean geometry, within a two-dimensional plane, for any given line L and a point A, not on L, there is exactly one line through A that does not intersect L—that is, a single parallel.
· In hyperbolic geometry, by contrast, there are infinitely many lines through A not intersecting L—an infinite number of parallels.
· And in elliptical geometry, there are no straight lines that do not intersect and, thus, no parallels.
Geometers have found a way to demonstrate that all of these geometries are logically consistent. First, they demonstrated that each of these geometries is can be represented in terms of any of the others. For example, elliptical geometry, in which there are no parallel lines, can be represented in terms of Euclidean geometry as the geometry of the surface of a sphere. On a Euclidean sphere, all straight lines are great circles, and all great circles intersect at two points, hence—no parallel lines. But this is just one example and, in fact, any one of the geometries can be represented in terms of any of the others. On the basis of this demonstration, and on the basis of the assumption that Euclidean geometry (having been tested by geometers for millennia) is logically consistent, they assumed that all of these geometries are consistent with themselves and do not lead to logical contradictions. This does not mean that Euclidean geometry is somehow more fundamental. It just means that mathematicians are so familiar with Euclidean geometry they are willing to assume that it is logically consistent, and that the ability to interpret these other geometries in Euclidean terms allows that same confidence to be extended to them.
However, we cannot decide through experiment which geometry actually applies to our particular physical universe. Although Einstein’s equations suggest that the space of our universe may be closed (that is, our geometry may be elliptical), the issue cannot be definitely resolved. The world that appears to us as Euclidean may, in fact, be governed by some other geometry or, indeed, by some much richer combination of multiple geometries.
Beyond this, it is possible to work out a consistent, but less restrictive, geometry in which parallel lines are entirely undefined. Note, that in this geometry, there are no units of measure (because measurement—in order to be consistent and, therefore, useful—always presupposes systems of parallel lines). A system without parallel lines is described by projective geometry, where all lines meet at one point—the “point at infinity”—which, paradoxically, is also right here at the focal point of our own perspective on the world.
Unless we can find some application for projective geometry, we might assume it is merely an intellectual construct with no possible application to actuality. In fact, there are two widely recognized valid applications for this theory.
· Projective geometry is the key to the art of perspective. In projective space, all parallel lines meet at the vanishing point. Thus, the space defined in visual perception is actually projective. The supreme accomplishment of the Euclidean understanding of space is that it allows a clear coordination between various perspectives. From my own point of view, I cannot consistently judge distance because a given visual object may be large and far away or small and close. If I can’t accurately judge distance, then I cannot deduce how an object that I see will appear to you. An accurate judgment of distance requires a framework within which various perspectives can be coordinated. If I know that you are three units away from me (in some particular direction as defined by some system of parallel lines), then I can mathematically transform my perspective into your perspective. Since projective space is the space of actual perception, the true function of metrical space is coordination of various perspectives. This is clearly illustrated in perspectival drawing, in which there are always two perspectives being coordinated—the vanishing point and a point just behind the eyes of the observer. Each of these is an instance of the one point at infinity.
· Projective geometry seems to characterize the time-space relation in many perceptual situations—for example, waking life, and some subset of our regular dreams, lucid dreams, and out-of-body experiences in which we occupy a body positioned in a time-space continuum somewhat similar to that of waking life. In those experiences, we find ourselves in a “scene,” surrounded by objects (such as buildings) and living entities (such as other people). In these scenes, we could draw a straight line from our point of view to each of those objects, so points and lines are clearly relevant to the time-space relation obtaining in those scenes, and yet measurable distance, as that property appears in waking life, does not apply in those scenes. For example, in dreams, objects come and go in ways that seems more relevant to feelings and meanings than to any measurable distance.
The point is that the creative advance of actual occasions not only doesn’t need a container (since each actual occasion houses all of its past), but it also doesn’t need a system of parallel lines to coordinate its various perspectives. Thus, the scientific idea that to be actual is to be measurable is clearly too limited.
Note that projective geometry is, logically, a more general system than metrical geometries. The latter are derived from projective geometry by first introducing a parallel postulate and, secondly, by establishing which of the known parallel postulates apply.
But projective geometry, itself, is derived from a time-space relation that is even more general and fundamental. Whitehead refers to it as “the extensive continuum.” The extensive continuum is a time-space relation in which “regions” are defined, but points and lines are not. In fact, Whitehead goes to considerable length to demonstrate that he can, by a process he calls “extensive abstraction,”[14] identify elements of the extensive continuum that can function as points and lines. While Whitehead’s logical exposition of this continuum is quite technical, we can get an intuitive sense of it by assuming the meaning of a “region,” and they by defining the extensive continuum as a relationship among regions such that:
1. Every region is extended over by other regions, and itself extends over other regions.
2. The relation of extension is transitive, such that if region A extends over region B, and region B extends over region C, then region A extends over region C.
3. If region A extends over region C, then there is a region B such that A extends over B and B extends over C.
4. If there are two regions A and B, there is a region C that extends over both.[15]
These extensive properties are intrinsic to all of our usual thinking about space. From the extensive continuum, we can derive a projective geometry by defining (or by deriving through extensive abstraction) points and lines. We can derive all metrical geometries from projective geometry by adding the relevant parallel postulate. Thus, within the extensive continuum, we can include both the worlds experienced in certain, clear lucid dreams and out-of-body experiences, as well as the continuum of waking life.
The important point, for our purposes, is that once we have articulated the properties of the extensive continuum, we have also opened up the possibility of considering time-space relations that are not continua at all, but rather are what I am calling “extensive networks.” In this case, the smooth properties that define a continuum are absent, and the connections among the actual occasions involved is rather more like the connection among computers on a peer-to-peer-network. In such a network, each computer is potentially contiguous to any other, but is actually in communication with some subset of the others in any given moment. Such a network would emerge if the second, third and fourth propositions which we used to define an extensive continuum above did do not apply. As discussed in Chapter 8, this is likely to be the type of time-space relation found in the mental world. In the vital world—where we experience actuality as various entities arrayed around us—we seem to be operating in more of a continuum. However, there are certain ways in which the vital worlds also have network-like properties.
It will be easier to understand the implications of extensive networks if we discuss them in terms of waking memory
· The time-space relation of waking memory is not extensive. Region A can extend over region B, and region B can extend over region C, but region A does not extend over region C. For example, I remember the event of my twenty-fifth birthday, and remember that on my birthday I recalled the words of a popular song sung by one my guests. Today, I cannot remember those words. I can remember an event during which I had a certain memory, without having that same memory now.
· It waking memory, it is not always possible to find a region between two other regions. This is exemplified in “recovered” memories. Something happened to me a long time ago, and I have forgotten it. Then, later, with the proper stimulus, the memory returns. I now have a direct memory of something that happened long ago, without having a memory of having remembered it at any point between now and then. In logical language, if region A extends over region C, then there may or may not be a region B such that A extends over B and B extends over C.
· In waking memory, it is not always possible to find a moment in which two earlier memories are both present. When I am in a “bad mood,” I may have certain memories of depressing events that I never remember when I am in a “good mood,” and vice versa. Again, in logical language, if there are two regions A and B, there may or may not be a region D that extends over both.
Because memories are organized in a network way, we usually think of them as “merely subjective.” But, as discussed earlier, in this new metaphysical approach, memories are direct, actual objectifications of past events in the present. We know that memories have definite causal effects in waking life and that, in many cases, the effect happens precisely when the memory occurs. For example, I am driving across town to a meeting, when I suddenly remember that I left the directions at home. This forces me to turn around. The memory was objectified in the moment of being remembered, and was not causally effective until that event.
Thus only certain very restricted portions of our experience—those that come through our waking physical senses—are entirely ordered by an extensive time-space relation. Our memory, for example, is not so ordered.
If we assume that actuality is a creative advance of causally interacting drops of experience (actual occasions), then we have no basis on which to deny actuality to the spaces we experience in alternative states of consciousness. A dream, no less than a moment of waking experience, consists of causally interacting drops of experience. The main differences between dreams and waking life are first, that the enduring entities in dreams are more variable in their behaviors than those in waking life; and, second, that the relations between them are much more complex, and are not subject to uniform relations of metrical distance. We can account for these differences by realizing that the occasions making up the enduring entities in dreams are of a higher grade than occasions making up the physical (inorganic world), and that they are, by their causal interactions, defining a time-space relation that is not part of the extensive continuum of waking life.
Our fixation on extensive continua is very much a function of what Jean Gebser[16] calls the “mental mutation” of consciousness—which is to say the structure of consciousness that has obtained since the “Athenian miracle” in approximately 500 B.C. This mutation, which brought us literacy, is correlated with extreme privileging of the visual sense.
It is interesting to note that each sensory mode has its own peculiar relationship to the actual world. Touch, taste, and smell are involved in very direct participation with the surrounding actuality. They rely on immediate proximity, and they convey variations of intensity, but they inform us very poorly about distance. Hearing, especially because we hear in stereo, gives us some sense of outer direction and some sense of distance. But only vision gives a clear, precise, and potentially measurable sense of direction and distance. Notice, too, that in taste, smell, and hearing, distinction between objects is weak. Different sensa belonging to different objects can easily be experienced as occupying the same time-space region—for example, many sounds can come from the same place. But the visual field is rather clearly tessellated by distinct, non-overlapping regions, and it is possible, within these regions, to bring attention to smaller and smaller regions up to the limits of our discrimination. Thus our privileging of sight leads to our idea that the “outer” world is dominated by relations of extension. As Gebser demonstrates in detail, earlier mutations of consciousness (for example, the “magical,” which accompanied hunting and gathering, and the “mythic,” which accompanied village agriculture) privileged hearing and speaking over vision, and thus made much less use of extension in defining the outer world.
The privileging of sight, and our heavy reliance on the extensive relations characteristic of the visual field has led us to a major discovery—that the time-space relation conditioning causal relations in the physical world is extensive. Indeed, it is metrically geometrical, so that it permits measurement. But this does not mean that all actuality is extensive and metrical in the same way.
In fact, I would like to suggest that we—the high-grade occasions making up our personalities—do not relate to the world through the same time-space relation that suffices for inorganic occasions. Rather our time-space relation to actuality is much more complex.
To make this clear, I want to say something about the nature of the perceptual process in terms of an ontology of actual occasions. Remember we are regarding the flow of energy in the universe as a transmission of experience through the creative advance. My sense organs experience the past experiences of actual occasions in the environment outside my body. Then the experiences of the sense organs are transmitted through the cellular occasions of the nervous system. These occasions are ordered into a hierarchy of grades, and, as the flow of experience proceeds up the hierarchy, the original sensory experiences are synthesized and interpreted. Eventually, some high-grade occasion performs a final synthesis for each sensory modality. These are what Buddhist psychology, for example, calls the “eye consciousness,” the “ear consciousness,” and so on. In each moment, the high-grade occasions synthesizing the various sensory consciousnesses, are objectified in me. At this moment, for example, the visual picture I see of the surrounding world is the objectification in me of what my eye consciousness experienced a split second ago. But where am I? Where is the mental grade occasion of experience that is me in any given moment of waking perception?
At this moment, here I am experiencing my eye consciousness—which has ordered its perception of the world in terms of a metrical geometry. I also have my other sense-consciousnesses—each of which has its own distinctive way of ordering the world. And I have my memories, which order the world in a network way, and include memories of dreams and, possibly, of lucid dreams and out-of-body-experiences—none of which took place anywhere in the physical world. So where am I? Does it really make sense to imagine that I am occupying a position in the metrical space defined by the inorganic occasions in which my body is embedded? It seems more as if I am somewhere outside that world, looking into it through my senses. My body is a kind of “avatar”[17] in the physical world through which the occasions of my personality operate. As a high-grade occasion, I have my actual existence in a transphysical world.
Summary
Let’s review the main points of this chapter:
· We saw that in an ontology of actual occasions each actuality contains or houses the entirety of its causal past. Each occasion, after completing its own concrescence, is then contained in future occasions. Thus, every actual occasion is an “atom” of time-space. No neutral time-space exists in its own right as a container for the process of actualization. Beyond actual occasions there is mere nothingness.
· We saw that a systematic relationship exists among actual occasions in any given society (where we consider even our evolving universe as a society of actual occasions). This relationship is the “geometry” of the time-space in that society, and it functions to:
o Establish a causal order among the relevant occasions, enabling them to be sorted into the immediate past, and into more distant regions of the past.
o Provide a scheme of indication enabling the various occasions in that society to refer to other particular occasions. This allows us to indicate, to point out, specific actualities in the environment. Also, because the various occasions involved in perception can indicate to one another that they refer to the same external actualities, it allows those occasions to bind their experiences together into a unified whole (as in the synthesis of data from various rods and cones in the eyes into a single picture, or in the synthesis of various sensory modalities into a single presented image of the surrounding world).
o Provides each new occasion a position within its region of the creative advance, determining the perspective of that occasion on its world.
o Governs the attenuation of causal efficacy with distance (as, for example, in the “inverse square” law governing gravitational attraction in Newtonian mechanics, which specifies the force of gravity as a function of distance).
· We saw that the time-space relation is a restriction on what is possible. For example, the four-dimensional continuum of relativity theory tells us where and when occasions belonging to the physical world can happen. If they take place outside that continuum, they are not, by definition, part of that world. Eternal objects are, in their nature, possibilities, and logic is a study of the systematic relations among eternal objects. We can treat the time-space relation as a logical structure, and explore it using methods of logic and mathematics.
· We also saw that logical systems may be more or less constrained by definitions and axioms. The greater the number of definitions and axioms, the more restricted are the possibilities that structure explores. The less constrained the time-space relation is, the freer it is, and the further it is from the narrowness of physical existence. Meta-geometry (which explores time-space relations that are less constrained than the metrical time-space governing inorganic occasions) maps the geometrical structures of the transphysical worlds.
· We clarified why (classical) measurement is possible only in a metrical time-space, in which a parallel postulate is specified. The time-space relation of the inorganic occasions of our cosmic epoch is metrical, which is why physics works so well in the physical world.
· We saw that projective geometry does not stipulate a parallel postulate, but that it does define points and lines. This is the time-space relation of perception—both in the waking world and in those parts of the transphysical worlds that most resemble the physical.
· We saw, too, that “extensive geometry” defines a particular set of relations among regions without defining points and lines. It is still more general than projective geometry.
· And we saw that “extensive networks” trace networks of relations among occasions that are not “smooth” and “continuous” in the way that extensive relations are. Non-metrical geometry functions between occasions in memory, and in many dreams that are too strange to remember clearly upon awakening. Interactions among occasions in most transphysical worlds define network geometries.
· Furthermore, we saw that the human personality (considered as a personally ordered society of high-grade actual occasions) inhabits a complex network time-space. Modern electronic technology can help us to visualize such a network. Imagine that our consciousness were embodied in a machine with the capacity to send and receive multiple streams of electromagnetic energy (for example, communicating via radio signals the way cell phones do). We could then be in contact with various other entities, none of whom would necessarily be in contact with each other. A world such as this would be very different from our world, but there is no metaphysical reason why such a world is impossible. It is in the context of non-metrical geometries that certain occasions in our past need not be felt, or positively prehended, in the present.
· We noted that the time-space of visual experience is extensive and projective, and that the time-space of physics is a framework for coordinating various perspectives into a shared world, that it is an extensive, metrical, geometrical continuum. But this is not the time-space of experience as a whole. Waking experience comprehends the various time-space relations characterizing the various senses, as well as the network time-space of memory, imagination, and dream.
Waking life, in what Jean Gebser called the “mental mutation” of consciousness, is characterized by a decisive privileging of the objectification of visual consciousness. Gebser, and others, suggested that we are moving into a new mutation of consciousness, less hypnotized by visual representation. The ideas presented in this chapter describe time-space in ways that are compatible with the new, or emerging, “integral mutation” of consciousness, as Gebser defined it.
In this and previous chapters, I have laid out the groundwork for a new metaphysical model that makes the idea of transphysical worlds intelligible, if not, indeed, plausible. Building on this, in the next chapter I will focus specifically what it means to be a human being, or a human personality, inhabiting the transphysical worlds.
33
[1] In the general theory of relativity, mass conditions space by changing its “curvature.” The curvature of space is a difficult notion that, fortunately, we will not have to deal with in this chapter. It is sometimes thought that relativity physics implies a subject because it talks about an observer. But, in relativity physics, what is relative is actually mathematically defined accelerating frames of reference. Whether or not those frames of reference are occupied by subjects is irrelevant to the theory itself.
[2] Ernst Cassirer, Substance and Function, Dover Publications, 1980.
[3] Whitehead articulated his philosophy science in various works, including: A. N. Whitehead, An Inquiry Concerning the Principles of Natural Knowledge New York: Dover Publications, 1982), A. N. Whitehead, Concept of Nature (Cambridge University Press, 1964), A. N. Whitehead, “The Principle of Relativity with Applications to Physical Science,” in Northrop, F.S.C. and Mason W. Gross, eds. Alfred North Whitehead: An Anthology, (New York: Macmillan, 1961), A. N. Whitehead, “Time, Space and Material; Are They, and If So in What Sense, the Ultimate Data of Science,” in Whitehead, Alfred North, The Interpretation of Science: Selected Essays, (Indianapolis: Bobbs-Merrill, 1961).
[4] I use “creative advance” here rather than the more familiar “time” because I am viewing time (as it is understood in the modern sense) as an abstraction from the process of creativity which issues in the ongoing actualization of occasions of experience.
[5] Whitehead, Process and Reality, Op Cit.,. 167.
[6] Whitehead refers to actual occasions as “atoms” of time-space. The word “atom,” however, carries so much metaphysical history that it would be somewhat misleading to use it in this context.
[7] Someone might be tempted to say “But what about the paper on which the drawing was done? Doesn’t that represent objective, outer space?” The answer to this question is no, since any area of the paper not apparently occupied by the largest parabola is to be imagined as contained within a still larger parabola that cannot, given the nature of the medium, be represented here.
[8] There is considerable confusion about this particular feature of special relativity. This is due to the following situation: If two occasions, A and B, both in the past of occasion C are too remote from each other to have causally interacted with one other, then occasion C may see either one as preceding the other depending on its own frame of reference. This does not change the fact that all causal relations that do, in fact, take place will be experienced by all future occasions as having that same causal order. The point is that special relativity, does not imply a “block universe” in which everything that ever will happen has, in some sense, already taken place. This confusion may arise from the fact that Einstein, who was a determinist in his thinking, did think of the universe as a four-dimensional block. But the fact that Einstein was, on philosophical grounds a determinist should not suggest that the Theory of Relativity,, itself, implies determinism. Clearly, it does not. For an excellent discussion of this point, see Chapter XI in Milik Capek, The Philosophical Impact of Contemporary Physics, Van Nostrand Reinhold Company, New York, 1961.
[9] There are, of course, non-local effects as well, but non-local effects are not the same as efficient causes. Non-local effects, as I understand them, instantaneously affect probabilities of other events, but they are not prehensions of actualities.
[10] Classical science has left us with the unfortunate habit of assuming that the only real efficient causes are those that come from the immediate past. But this notion is undermined by quantum theory, which says that all causal transmission of effects through time can be described by the Schrödinger wave function, which, because it is a linear equation, never loses any information. Thus, in quantum mechanics, an effect from the distant past may be transmitted, entirely unchanged and unexperienced by any intervening occasions, through the creative advance, indefinitely—until the right conditions emerge under which it can be expressed.
[11] Whitehead discusses this idea at length in Science and the Modern World, Free Press, 1997, Chapter X. I have written a commentary on this chapter, accepted for publication in Process Studies Supplements, at http://www.ctr4process.org/publications/ProcessStudies/PSS/. It can now be found at: https://ericweiss.com/a-commentary-on-chapter-ten-of-science-and-the-modern-world-by-alfred-north-whitehead.
[12] Certain modern ideas of “information” that suppose it can be quantified in terms of bits seem to me to miss the point. Even if the “information” contained in an event could be expressed as a very large set of yes/no questions and answers, all of the really interesting information is contained in the questions themselves. The answer to the question “is it red or blue?” is irrelevant if I don’t know the meaning of redness and blueness. I suspect that all of this talk in the scientific literature about “information” is an attempt to get at the relevance of eternal objects to actuality. I am using the word information to convey the operation of eternal objects to form, or to “inform” events.
[13], Bernard Russell, Introduction to Mathematical Philosophy, London:George Allen and Unwin Ltd., 1953, p. 5-6.
[14] Whitehead discusses this method in An Inquiry Concerning the Principles of Natural Knowledge, New York: Dover Publications, 1982, p. 101-109 and Process and Reality, corrected ed. New York: The Free Press, 1985, p. 294-333.
[15] Note that these propositions, as stated, are not sufficiently technical to be logically adequate. For a fuller presentation of the actual propositions involved see the sections pointed to in the preceding footnote.
[16] Jean Gebser, The Ever-Present Origin, trans. Noel Barstad with Algis Mickunas, Athens, Ohio: Ohio University Press, 1985.
[17] Here, I am borrowing the word “avatar” from computer gaming, where it refers to the “person” on the screen who represents me and whose actions reflect my decisions. Computer gamers, in turn, borrowed this word from Vedic cosmology, in which a Divine Avatar is a physical vehicle through which the Divine expresses itself in the historical or evolutionary process.